2種類のグループA,Bがあり、その人数の比はA:B=1:2である。
今、14人がBからAに移ったので、その比は5:7となった。
A,B合わせて人数は何人か?
これは2020年度の愛知県公立高校入試の問題を簡略化したものです。
これをどう解くか、想像がつきますか?
普通に解くのであれば、Aグループの人数をx、Bグループの人数をyとおいて、
x:y=1:2
x+14:y-14=5:7
より、
y=2x
5(y-14)=7(x+14)
これらを連立して解けば、(x,y=56,112)という答えが出ます。
しかしながら、比のなんたるかを理解していれば、実は裏技的な手法を使ってもう少し簡単に解くことも可能です。
この話は、過去の「異なる尺度の比を同一の尺度の比に直す方法」という記事にも関連しています。
まずは、例題として「AとBの人数比が3:2だったのが、BからAに10人移動したことにより4:1となった」場合を考えてみましょう。
この場合、「3:2」と「4:1」はどちらも同一の尺度で考えることができます。「同一の尺度」とは、「比でいうところの『1』にあたる実際の数が同じである」ということを指します(下図参照)。
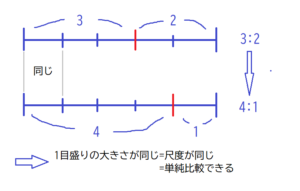
そのため、「10人移動したことにより3:2が4:1になった」ということは、比でいうところの『1』(上の図の1目盛り)がそのまま10人に該当するということです。したがって、この例題においては、両グループ合わせて50人いるという答えを出すことができます。
ところが、元の問題では尺度が異なるため、この手法が使えません(下図参照)。
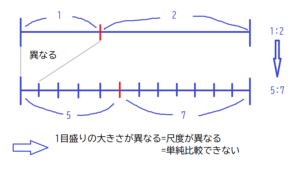
では、どうしたらよいかというと、尺度が異なるのであれば尺度を揃えてやればよいのです。
例えば、a:bとc:dの尺度を揃えたいのであれば、
①a+bとc+dの最小公倍数を求める(1+2=3、5+7=12 →3と12の最小公倍数は12)
②その最小公倍数をa:bとc:dに分けた時の比をそれぞれ求める(12を1:2に分けると4:8、5:7はそのまま)
この2ステップによって出てきた比が、「尺度の揃った比」となります(下図参照)
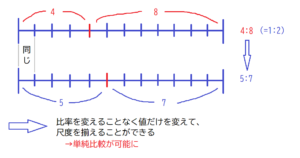
したがって、「14人移動したことにより4:8が5:7になった」ということは、上図でいうところの1目盛りが14人にあたることを意味しています。
全体の人数は、この1目盛り14人が12目盛り分あるので、14×12=168
ということで、168人という答えを導き出すことができます。
比の扱いに慣れていないのであれば連立方程式を利用する方が確実でしょうが、逆にここで紹介した手法を使いこなすことができれば、この問題を暗算で解くことすら可能です。
余裕のある人は、ぜひ覚えておいてください。

