とある中学校の2年生にユニークな図形問題が出題されたので、解説していきたいと思います
下のような図形を凹六角形という。
下の図を利用し、この凹六角形と同じ面積の四角形を作図せよ。
※コンパス、定規は使用可
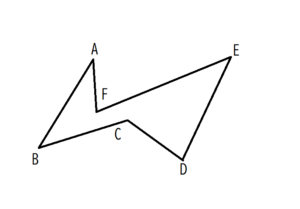
発想力が試される問題です。中学2年生までの図形の知識で解くことができます(ただし、中学1年生でも解くことができます)。
それでは、考えてみましょう

【解法】
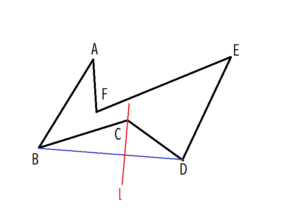
①まず、下図のようにBDに補助線を引き、Cを通りBDに垂直な線をコンパスを用いて作図します。この垂線を直線lとします。
(作図方法はここでは割愛しますが、中学1年生で学習しています)
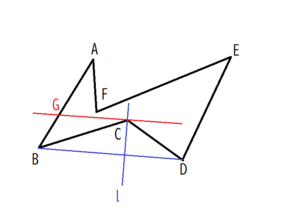
②続いて、Cを通り直線lに垂直な線を作図します。この線はBDに平行となります。その平行線とABとが交わる点をGとします。
③同様の手順で、AEに平行な直線を作図し、その線とEDとの交点をHとします。
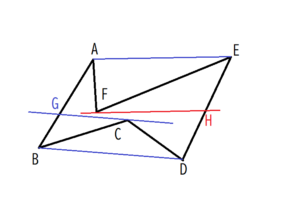
④最後に、DとG、AとHをそれぞれ線で結びます。出来上がった四角形AGDHは、元の凹六角形と同じ面積になっています。
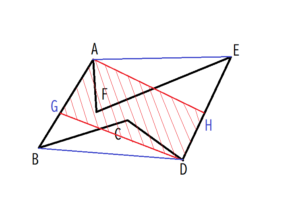
【解説】
問題の凹六角形の面積は、四角形ABDEの面積から△BCDと△AEFの面積を引いたものになります。
また、BDとCG、AEとFHがそれぞれ平行であることにより、△BCD=△BDG、△AEF=△AEHが成り立ちます(底辺が共通で、かつ頂点が平行線上にあることから高さも等しいため)。
以上のことから、
四角形ABDE-(△BCD+△AEF)=四角形ABDE-(△BDG+△AEH)
. =四角形AGDH
より、元の凹六角形と四角形AGDHが等しいということが証明できます。

