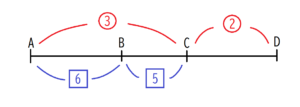
上の図のように、AC:CD=3:2、AB:BC=6:5となる4点A,B,C,Dが一直線上に存在する。この時、BC:CDの値をもっとも簡単な整数の比で求めよ。
類似の問題が中3の図形の単元で出題され、解くのに苦労している様子が見られたので解説を加えます。
まず、AB:BC=6:5より、AB:BC:AC=6:5:11
したがって、AC:CDは3:2と表される一方で、11:xという形でも表さるということが分かります。これらは同じAC:CDという比を表しているので、3:2=11:xと比例式を立てることができます。
これを解くと、x=22/3 よってBC:CD=5:22/3
「もっとも簡単な整数の比で」という指示があるので、BC:CD=15:22
比の扱いについては、とりあえず内項の積と外項の積で方程式を立てるという手順を頭に入れている人も多いと思いますが、このような応用も利かせられるようになるとよりステップアップが望めます。

