東郷町・日進市の個別指導塾
「個別指導塾ピックアップ」
日進東郷校担当の、志野 瑞季です。
こんにちは!!
「本日は頭の体操」ということで
小学5年生の面積の問題をやっていきたいと思います!
問題はこちらです!
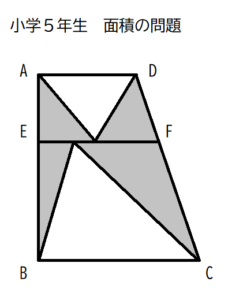
四角形ABCDは台形で高さが15cm、
下底の長さが18cmで、辺EFは辺AD、辺BCと並行で12cm。
では影を付けた所の面積はいくつでしょう。
こちらの、一見どう解くかが全く分からないような問題ですが、
台形ということに囚われてしまったり、比で考えようとすると失敗してしまいます。
ちなみに台形の面積の公式は(上底+下底)×高さ÷2ですが、
台形の面積から影のついていない三角形二つの面積を引けば出そうでも
当てはめていっても面積が分かっていない、わからないためうまく出てきません。
頭が痛くなってきますね……
ではどうやって解いていくのでしょうか。
ヒントは三角形にあります。
勘のいい方なら気づいていたかもしれませんが、この台形の中に三角形が4つあるんです……!!
N字型の影ですが、真ん中の辺EFによって分断されています。
仮にこの辺EF上にある点を点G、点Hとしましょう。
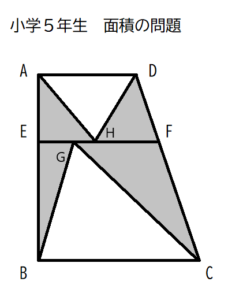
すると、△AEH、△DFH、△BEG、△CFGという三角形が4つ見えてきました!
あとは、三角形の面積を求めるだけです。
まず、上の三角形ですが、辺EFを二分したものを底辺とした三角形が二つ、
そして下の三角形も辺EFを二分したものを底辺とした三角形が二つ。
辺EG+辺GF=12cm、そして辺EH+辺HF=12cmです。
ということは、上の三角形も下の三角形も底辺が12cmの三角形が一つ分ずつになりますね。
最後に必要なのが辺AD~辺EFまで、辺EF~BCまでの高さです。
それぞれは分かりませんが、合計すると15cmということが分かっています。
つまり、上と下の三角形を全て足すと、底辺12cm×高さ15cm÷2
12×15÷2で答えが出るということになり、答えは90cm²となります!
求め方が分かるとスパッと解けますが、
考え方を4つの三角形にフォーカスしなければ難しかったですね。
このような問題を中学生には息抜きとして、
小学生には難問として時々出しています!
気になった方は下のリンクからぜひ体験にきてみてください!

